Prácticamente todos los fotógrafos conocen la expresión «factor de recorte» (a veces también llamado «factor de multiplicación de la distancia focal» o «magnificación de la distancia focal»). Muchos de ellos son vagamente conscientes de que representa el tamaño relativo del sensor comparado con el de un fotograma de una película analógica. Aún menos son los que saben la forma en que influye exactamente en el resultado de las fotos tomadas con teléfonos, cámaras compactas, y cámaras APS-C DSLR; en comparación con una cámara full frame o de fotograma completo. Pese a todo, las diferencias pueden ser bastante sorprendentes. Lo notaremos en lo referente a la distancia focal, la velocidad de la lente y la nitidez.

Probablemente hayas notado que se pueden obtener imágenes significativamente diferentes utilizando la misma exposición (apertura, velocidad e ISO) en diferentes cámaras. Especialmente en lo que respecta a la profundidad de campo. Esto es claramente visible cuando comparamos ejemplos de extremos opuestos del espectro: una réflex digital de fotograma completo con un smartphone.

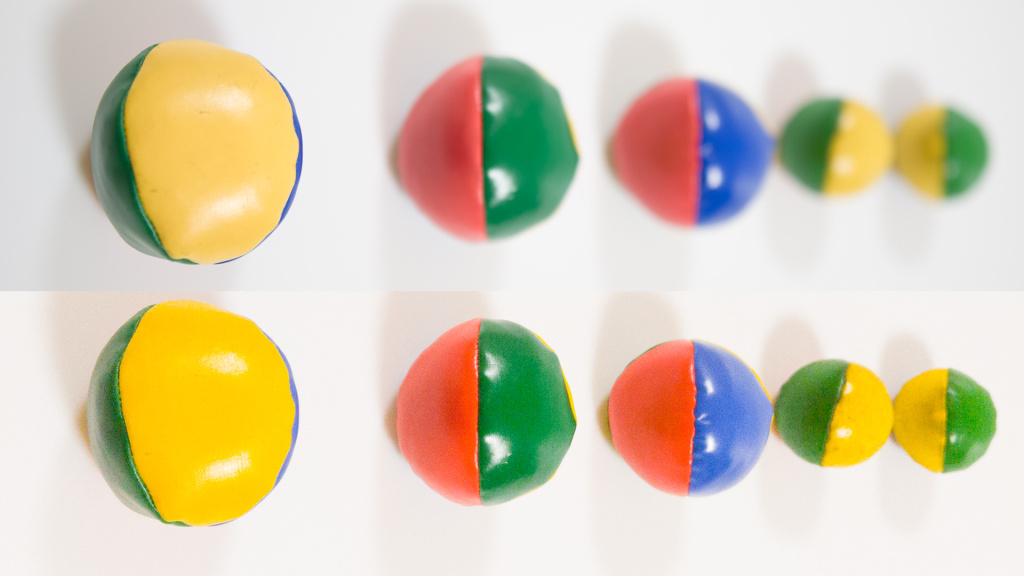
La imagen de arriba muestra los resultados de una cámara full frame Canon 5D Mark IV DSLR y un LG G4, ambos con un ángulo de visión similar y con una configuración similar de la apertura (f / 2 para la DSLR y f / 1,8 para el teléfono). La imagen de la cámara réflex digital, en comparación, tiene un fondo mucho más borroso.

Hay múltiples factores que influyen en las diferencias entre los dispositivos. Pero todos ellos tienen el mismo origen: los diferentes tamaños de los sensores y de las lentes. , Estos tamaños y las propiedades que resultan de ellos se definen por el factor de recorte.

El factor de recorte puede revelar el tamaño del sensor

Cualquier fabricante de hardware puede hacer un sensor de tamaño arbitrario (y de facto, lo hacen). Debido a que el tamaño importa, la hoja de especificaciones de la cámara casi siempre mencionará la anchura y la altura del sensor en milímetros (por ejemplo, 36 x 24 mm) o en diagonal.

Por desgracia, por razones históricas, esta no es la diagonal del sensor, sino más bien, la del tubo de rayos catódicos (CRT) al que equivaldría en la era de las cámaras analógicas. Por lo tanto, es un poco mayor que el sensor. Se da en fracciones de pulgada (por ejemplo: 1/4”).

Debido a que es difícil comparar sensores, y más difícil aún es comparar las lentes montadas sobre ellos, se introdujo un factor de comparación relativa que facilitase la labor .Y eso es lo que representa el factor de recorte.

El factor de recorte expresa cuántas veces más pequeño (u ocasionalmente, más grande) es un sensor, comparado con el tamaño de un fotograma de película de 35 mm medido en diagonal. Cuanto mayor sea el factor de recorte, menor será el sensor.

Smartphones: sensores hasta 36× más pequeños que el fotograma completo

Los sensores de tipo full frame o de fotograma completo, tienen un factor de recorte de 1 y son la referencia para el resto de factores de recorte.

Los sensores más pequeños tienen un factor de recorte superior a 1.Las Réflex digitales típicas, tienen un factor de 1.5 o 1.6, las cámaras sin espejo 2, y los sensores de los smartphones tienen alrededor de 6. Así que, un teléfono inteligente tiene un sensor con una diagonal unas 6 veces menor que las DSLR full frame y un área unas 36 veces menor (aproximadamente, ya que pueden tener diferentes relaciones de lados).

Mientras tanto, en las cámaras medianas y de mayor formato, los sensores son más grandes que en las de fotograma completo y por lo tanto, tienen un factor de recorte de menos de 1 (típicamente de 0,5 a 0,8).

El factor de recorte te ayuda a saber qué es cada cosa en las lentes

El cuadro siguiente ilustra dos sistemas diferentes con dos tamaños diferentes de sensores y con dos lentes que tienen un ángulo de visión idéntico. Sin embargo, lo que se presenta como el principal parámetro de las lentes es la distancia focal. Se indica con una f, y representa la distancia desde el sensor al centro óptico de la lente.

Nótese, que para conseguir el mismo ángulo de visión, las lentes necesitan distancias focales significativamente diferentes para los diferentes tamaños de sensor:

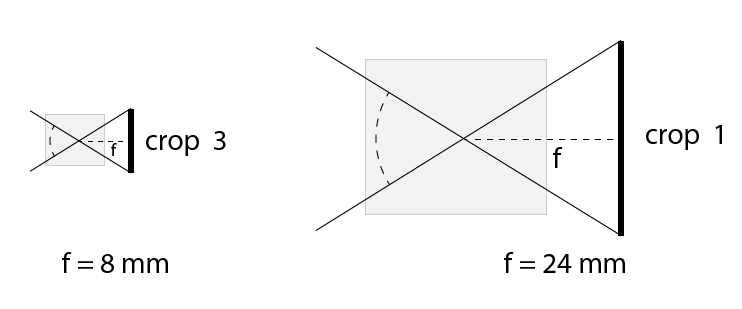
A pesar de que el ángulo de visión se puede calcular a partir del tamaño del sensor y de la distancia focal, es más fácil simplemente multiplicar la distancia focal por el factor de recorte. Esto nos da la distancia focal equivalente. Lo que esto nos dice, es que la lente dada tiene el mismo ángulo de visión que tendría otra lente en sensor de tipo fotograma completo.

Por ejemplo, una lente de 8 mm en un sensor con un factor de recorte de 3 es equivalente a una lente de 24 mm en un sensor de fotograma completo (8 mm x 3 = 24 mm).

El factor de recorte también influye en la velocidad de la lente

Tenemos un par de cosas más que decir sobre las lentes. La luz no pasa solamente a través del único punto medio tal y como se muestra en la imagen anterior, así que las hojas de especificaciones dan un valor de apertura que describe la velocidad de la lente. Dicho parámetro se escribe como f / X, donde X es un número, y el verdadero significado es «distancia focal dividida por X».

El resultado es el tamaño del orificio a través del cual pasa la luz en el centro de la lente. Por ejemplo, un valor de apertura de f / 2,8 en una lente con una distancia focal de 8 mm significa que el tamaño de apertura es de 8 mm / 2,8 = 2,9 mm.

Si utilizamos el mismo sistema que en el ejemplo anterior, con el factor de recorte de 3, y si nuestra lente equivale a una lente de 24 mm en un marco completo; entonces, hay que tener en cuenta que esta conversión sólo nos da el ángulo de visión. No podemos decir que equivalga a una lente de 24 / 2,8, que tendría una apertura mucho más grande (8,6 mm); sino que también tenemos que multiplicar el valor de apertura por el factor de recorte.

Así que, en el ejemplo, la lente 8 / 2.8 es equivalente a una lente de 24 / 8,4 en un sensor de fotograma completo. Las imágenes de dos cámaras con dichas combinaciones de sensores + lente, serán casi indistinguibles, simplemente, darán diferentes niveles de ruido en determinados casos.

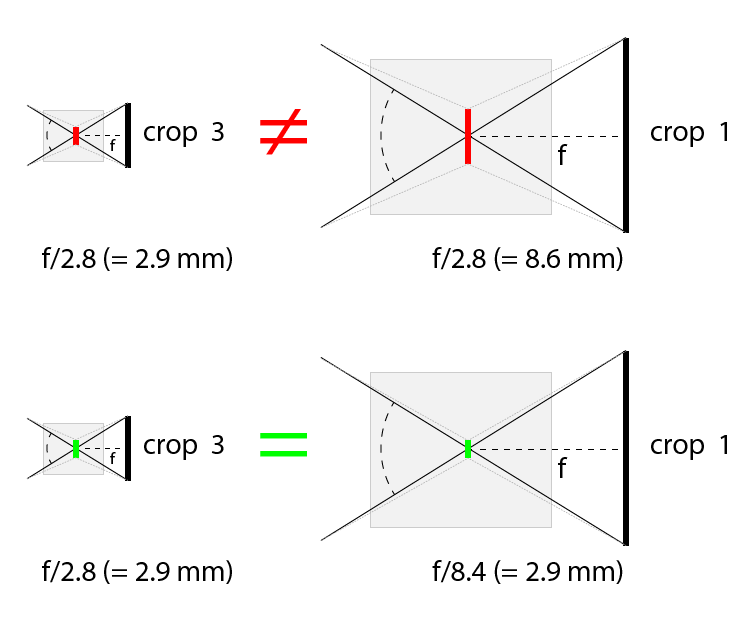
No hay que dejarse engañar pensando que basta con utilizar una apertura completamente diferente en sistemas diferentes para que el resultado sea equivalente. Está claro que, con valores más altos de la apertura, tendremos que utilizar una exposición mucho más larga o una ISO superior.

Esta discrepancia aparente está causada por el hecho de que la ISO está también relacionada con el tamaño del sensor; para diferentes sensores, el mismo valor conduce a una sensibilidad diferente y diferentes niveles de ruido. Para tener una visión completa del problema, podemos señalar que se puede conseguir que las fotos sean prácticamente indistinguibles mediante el uso de los siguientes parámetros:

• Sistema con factor de recorte 3: Distancia focal 8 mm, Abertura f / 2.8, ISO 100, velocidad 1/100 s
• Sistema con factor de recorte 1: Distancia focal 24 mm, abertura f / 8.4, ISO 100, velocidad 1/100 s

La misma toma con sensores diferentes

Tomamos aproximadamente la misma toma en cuatro sistemas con diferentes factores de recorte. Las cámaras tienen diferentes relaciones de lados, pero aproximadamente el mismo ángulo de visión. Nótese cómo difieren sustancialmente sus distancias focales:

En todos estos casos, la distancia focal multiplicada por el factor de recorte es de unos 28 o 29 mm.

Lo que hace que los sensores grandes sean mejores

A pesar de que se dice que un sensor más grande conduce a un menor ruido y es capaz de tomar fotos con una oscuridad mayor, la cosa es algo más complicada. Eso es porque dichas ventajas, en realidad no se deben al sensor, sino al objetivo utilizado. Si utilizamos una lente con un valor de apertura de, por ejemplo, 2.8 en dos sensores diferentes, para cada uno, representará valores diferentes del diámetro de la lente, por lo que dejará pasar una cantidad de luz diferente.

De manera que, con un sensor grande, es fácil tomar fotografías cuando hay una oscuridad mayor, ya que llega al sensor mucha más luz. Pero, en realidad, un sensor menor podría dar un buen resultado si utilizásemos una lente más grande y si pusiésemos una lente de aumento (como una «lupa») detrás. Esto existe, y se trata precisamente de un producto llamado MetaBones SpeedBooster.

Entonces, ¿hay algo en lo que un sensor de gran tamaño sea mejor? Sí, en su rango dinámico, ya que es mayor. Esto se debe a que es menos susceptible que un sensor pequeño, por lo que puede exponer una toma durante un tiempo más largo sin provocar quemados o cielos completamente blancos. Así que, es más fácil, por ejemplo, disparar a contra luz. La tecnología sigue su marcha, e incluso los sensores más pequeños, poco a poco, están mejorando, consiguiendo un rango dinámico cada vez mayor. No obstante, estas mejoras se aplican también a los sensores más grandes.

En este caso, hay una segunda ventaja digna de mención. Para los sensores de mayor tamaño es posible encontrar también lentes grandes y pesadas con excelentes velocidades. Pero los mencionados MetaBones SpeedBoster pueden hacer que lentes como esas se puedan usar también con sensores más pequeños, preservando casi las mismas propiedades ópticas de las lentes normales.

Lo que hace que un sensor grande sea mejor para la misma velocidad de la lente

Digamos que queremos comparar el mismo ángulo de visión y, además, un valor idéntico de la apertura (tal y como está escrito en las especificaciones de la lente). Entonces, estaremos comparando objetivos con diferente tamaño del orificios de entrada, por lo que para ambas combinaciones, es válida la siguiente regla: cuanto menor sea el factor de recorte (es decir, cuanto mayor sea el sensor) menor será la profundidad de campo y el menor el nivel de ruido.

A continuación, se muestran ejemplos con varios sistemas. Aquí no he incluido el smartphone, porque no permitía ofrecer una abertura equivalente a los otros dispositivos. Para las otras cámaras, utilicé una abertura de f / 2.8 y una distancia focal que corresponde a un ángulo de visión de 28 mm en fotograma completo.

Aquí la exposición era de f / 2.8 / ISO 800 / 1/60 s en todas. La ilustración muestra, de izquierda a derecha:

• Fujifilm XQ2 con una distancia focal de 6.4 mm, apertura después de multiplicar por el factor de recorte equivalente a f / 2.8 × 3.93 = f / 11 en fotograma completo.
• Canon 350D con una distancia focal de 17 mm, apertura equivalente a f / 2.8 × 1.62 = f / 4.5 en fotograma completo.
• Canon 5D Mark IV con una distancia focal de 28 mm, con una apertura de f / 2.8 (con un factor de recorte de 1).

Aquí es fácil ver la profundidad de campo; el sistema con el sensor más grande (pero sobre todo, con la lente grande) es el mejor en este caso.

La misma distancia focal en diferentes sensores

Para proporcionar una idea completa, incluyo también un ejemplo del efecto del factor de recorte cuando una distancia focal numéricamente idéntica se utiliza con sensores diferentes. Aquí se trata de una distancia focal de unos 25-26 mm.

Una comparación de los primeros y últimos ejemplos es la siguiente:

Si tuviéramos que juzgar basándonos estrictamente en este ejemplo, el factor de recorte funcionaría hasta valores de aproximadamente 3.7, pero esta imprecisión proviene del redondeo y de las diferentes proporciones de los lados.

Unos pocos ejemplos de lentes equivalentes

En muchos equipos encontraremos lentes similares, aunque con designaciones numéricas completamente diferentes. Pero basta con multiplicar la distancia focal por la apertura y por el factor de recorte para obtener lentes comparables. En otros muchos, podemos también comprobar que este tipo de equivalencias implican también tamaños y pesos similares.

Siempre es posible encontrar contraejemplos, tales como Microsoft Sigma 50 / 1.4 y la Canon 50 / 1.4 ambos con cámaras de fotograma completo, sin embargo, completamente diferentes en peso (811 g frente a 290).

Pero por lo demás, se puede encontrar una gran cantidad de lentes que proporcionan resultados similares, por ejemplo:

La Panasonic 14-50 / 2.8-3.5 para Micro Four Thirds (factor de recorte 2) pesa 490 g y equivale a una 28-100 / 5,6-7 a fotograma completo. Podemos encontrar lentes similares para fotograma completo fabricadas por el trío Sony, Nikon, Canon; todas ellas con parámetros algo mejores y consecuentemente, un poco más pesadas. Tal es el caso de Sony Microsoft FE 24-105 / 4 con un peso de 660 g.

Del mismo modo, la Sigma 50-100 / 1,8 para sensores APS-C (factor de recorte de aproximadamente 1.5) con un peso de 1.5 kg, corresponde a una 100-200 / 2,7 en fotograma completo. Sin embargo, lentes similares del tipo 70-200 / 2.8 existen desde hace mucho tiempo y análogamente, los principales fabricantes de cámaras de fotograma completo ofrecen productos equivalentes. Todos los ejemplos para este caso, pesan entre 1.3 y 1.5 kg.

La lente es lo que cuenta

Aunque el tamaño del sensor desempeña un cierto papel, el de la lente es mucho más importante. Entender el factor de recorte nos ayudará a entender las lentes y a juzgar diferentes combinaciones. Pero tener factores de recorte y valores de apertura más bajos, no siempre es una ventaja.

Si por ejemplo, estamos haciendo fotografías con una gran apertura, pero las queremos para colgar en la web con baja resolución, es casi irrelevante si llevamos una cámara de fotograma completo con una lente pesada, o una cámara compacta que nos cabe en el bolsillo.

Lo que es importante es ser capaz de juzgar cuáles son las ventajas y desventajas de un determinado artículo y decidir si es una buena opción, teniendo en cuenta el uso que le queramos dar.